https://www.acmicpc.net/problem/2565
2565번: 전깃줄
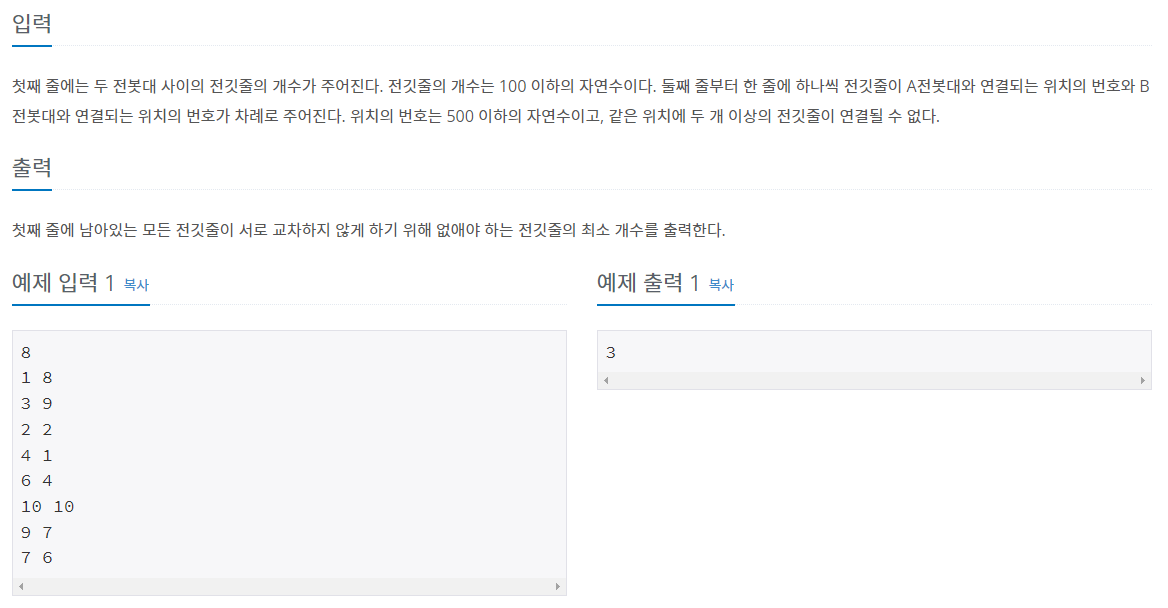
첫째 줄에는 두 전봇대 사이의 전깃줄의 개수가 주어진다. 전깃줄의 개수는 100 이하의 자연수이다. 둘째 줄부터 한 줄에 하나씩 전깃줄이 A전봇대와 연결되는 위치의 번호와 B전봇대와 연결되는
www.acmicpc.net
백준 사이트의 2565번 전깃줄이라는 문제입니다.

문제 설명은 간단하지만 막상 풀이 방법을 떠올리려면 떠오르지 않는 문제입니다.
솔직히 말하면 저도... 검색을 통해 다른 사람들의 풀이를 보고 풀었는데, 이 문제는 LIS(Longest Increase Subsequence)의 응용문제로 DP와 이분 탐색 두 가지의 방법으로 풀이가 가능합니다.
DP의 경우 구현과 이해가 쉽지만 입력의 갯수가 많으면 시간 초과로 문제를 틀릴 가능성이 있다는데,
마침 문제가 입력의 갯수가 100개인 전깃줄 1과 10만 개인 전깃줄 2로 나뉘어 있으니 두 가지 방법을 각각 활용해서 풀어보도록 하겠습니다. 먼저 DP를 활용한 풀이 방법을 보겠습니다.
개념은 간단합니다, 전깃줄이 같은 곳에 걸쳐있지 않는다는 조건을 활용하여 입력을 정렬하고, 사용할 전깃줄의 갯수를 하나씩 늘려가며 전깃줄의 부분집합이 만들 수 있는 최댓값을 기록합니다. 이때 구한 최댓값을 DP 배열에 저장하고, 다음 풀이에서 활용할 수 있습니다.
예제 입력을 통해 확인해 보겠습니다.
(1,8), (3,9), (2,2) ,(4,1), (6,4), (10,10), (9,7), (7,6) 이렇게 8개의 전깃줄이 들어왔습니다.
이를 전깃줄의 시작 위치를 기준으로 정렬하면
(1,8), (2,2) ,(3,9), (4,1), (6,4), (7,6), (9,7), (10,10)와 같은 형태가 됩니다. 진행 방향은 상관이 없지만, 저는 뒤에서부터 쌓아가며 진행하도록 하겠습니다.
(10,10) 하나를 추가하고 -> 이때의 LIS길이는 당연히 1이 됩니다.

(9,7)를 추가하고 -> 9,7 전깃줄과 10,10 전깃줄은 겹치지 않으므로 아까 구한 LIS 길이에 1을 더해 2가 됩니다.
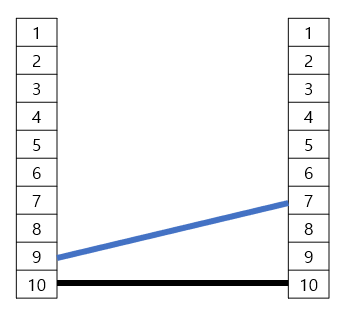
같은 방법으로 (4,1), (6,4), (7,6), (9,7), (10,10) 까지는 전깃줄이 겹치지 않고 LIS길이가 계속 늘어 5가 됩니다.
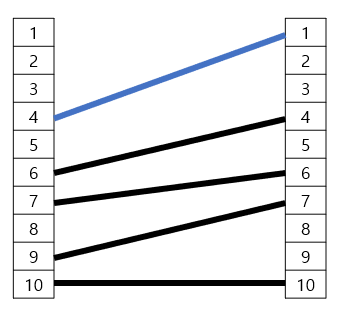
이 상태에 (3,9) 전깃줄을 추가하면 겹치는 부분이 발생하게 됩니다.
겹치는 영역은 (4,1), (6,4), (7,6), (9,7) 네 전깃줄로 (3,9)와 공존이 가능한 전깃줄은 (10,10) 뿐이고 그때의 LIS 길이에 1을 더한 2가 (3,9)를 포함한 LIS의 길이가 됩니다.

같은 방법으로 (2,2)를 추가했을때는 (2,2)다음으로 올 수 있는 전깃줄이 (6,4)로 (6,4)때 구한 값 4에 1을 더한 5를 얻고

(1,8)을 추가했을때는 (1,8), (3,9), (10,10)의 LIS가 구해집니다.

모든 경우에서 최댓값을 찾으면 예제에서 구할 수 있는 LIS의 길이는 5로 두가지 경우인 것을 알 수 있습니다.
이를 코드로 구현하면,
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;
public class Main {
static StringTokenizer st;
public static void main(String[] args) throws NumberFormatException, IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
int[][] wires = new int[N][2];
for (int n = 0; n < N; n++) {
st = new StringTokenizer(br.readLine());
wires[n][0] = Integer.parseInt(st.nextToken());
wires[n][1] = Integer.parseInt(st.nextToken());
}
Arrays.sort(wires, (e1, e2) -> {
return e1[0] - e2[0];
});
int[] dp = new int[N];
for (int n = N - 1; n >= 0; n--) {
dp[n] = 1;
int end = wires[n][1];
for (int m = n; m < N; m++) {
if (wires[m][1] > end) {
dp[n] = Math.max(dp[n], 1 + dp[m]);
}
}
}
int max = 0;
for (int n = 0; n < N; n++) {
max = Math.max(max, dp[n]);
}
System.out.println(N - max);
}
}이렇게 작성 할 수 있을것 같습니다. 감사합니다.
곧 전깃줄2 문제도 풀도록 하겠습니다.
'🔍 알고리즘 > 백준 Java' 카테고리의 다른 글
| [JAVA] 백준 18248번. 제야의종 (실버2) (0) | 2021.11.30 |
|---|---|
| [JAVA] 백준 4600번. 정글의법칙 (실버2) (0) | 2021.11.30 |
| [JAVA] 백준 1958번. LCS 3 (골드3) (0) | 2021.11.29 |
| [JAVA] 백준 9252번. LCS 2 (골드5) (0) | 2021.11.28 |
| [JAVA] 백준 9251번. LCS (골드5) (0) | 2021.11.28 |
