내일은 알고리즘

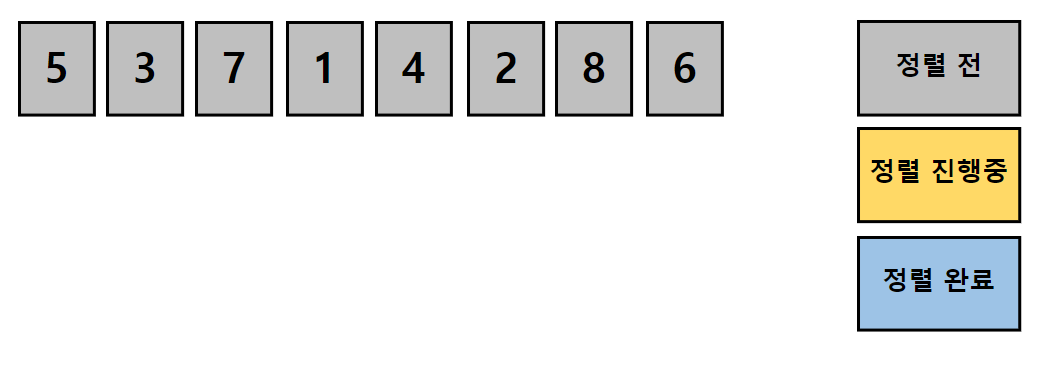
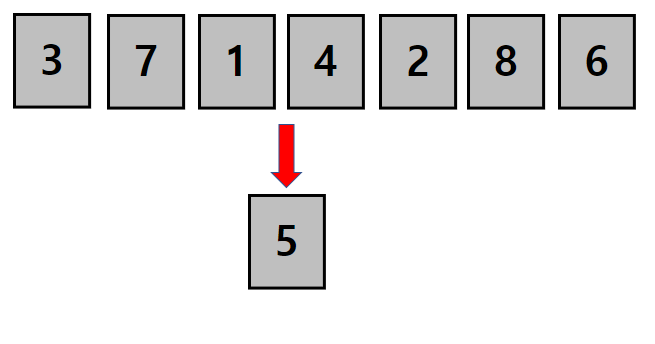
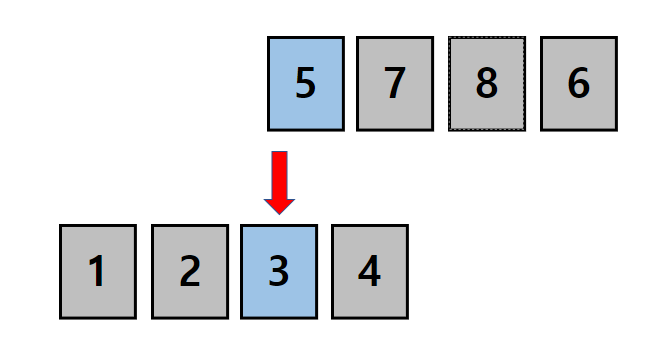
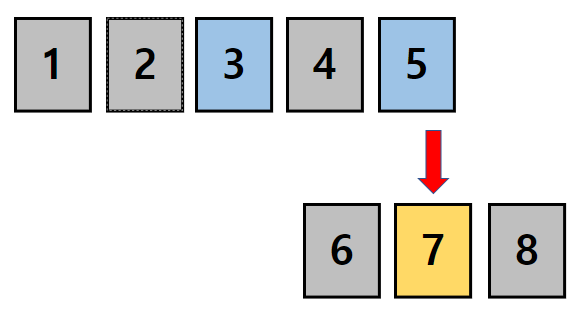
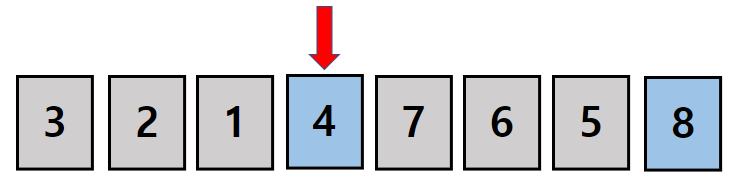
순열은 어떤 집합의 원소들을 중복없이 뽑아 순서에 상관있게 나열하는것입니다.

n개의 원소를 가진 집합에서 r개를 뽑아 순열을 만든다고 하면 nPr 과 같이 나타냅니다.

원소를 넣을지 말지를 정했던 부분집합과 달리 순열은 이 위치에 이 원소를 넣을지 말지를 나누어서 진행됩니다.

{1,2,3,4}로 4개의 원소를 가진 집합에서 4개를 뽑아 만들 수 있는 순열을 모두 구한다고 해봅시다. = 4P4

우선 첫번째 위치에 1이 들어갑니다.

이 과정에서 우리는 1로 시작하는 모든 순열을 구하게 됩니다. (1로 만들수 있는 경우)

중복이 허용되지 않기 때문에 이미 사용된 1을 제외한 나머지 원소들 중에서 두번째 자리에 들어갈 것을 정해야합니다.

순서대로 2를 넣어줍니다. (1-2로 만들수 있는 경우)

같은 방식으로 중복이 되지 않게 다음 자리에 넣어질 수를 구해봅시다.

이때 재귀 호출된 함수는 이런 상태입니다. 

가장 위쪽에서부터 하나씩 숫자를 선택하며 4번째 같은 함수를 호출했습니다.

원했던 4개의 원소를 뽑았으므로 1-2-3-4 순열이 완성됩니다. (1-2-3 으로 만들수 있는 경우)

이제 4번째 함수는 종료되고 세번째 함수로 돌아갑니다. (1-2로 만들수 있는 경우)

세번째 자리에 3을 넣은 경우는 앞에서 시행했으므로 이번엔 4가 들어갑니다.

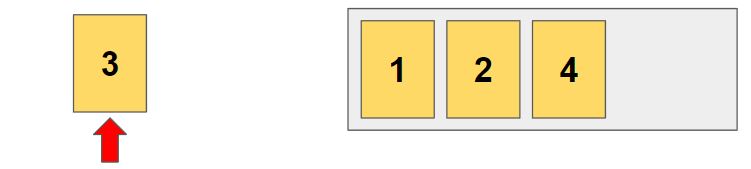
같은 방식으로 진행해서 이번엔 1-2-4-3 이라는 순열을 완성했습니다. (1-2-4 로 만들수 있는 경우)

순열은 구성한 원소가 같더라도 순서가 다르면 다른 것으로 보기때문에 1-2-3-4와 1-2-4-3은 다른 순열입니다.

첫 자리와 두번째 자리가 각각 1, 2인 경우는 모두 탐색되었습니다.

이제 두번째 자리가 달라지는 경우를 찾습니다.

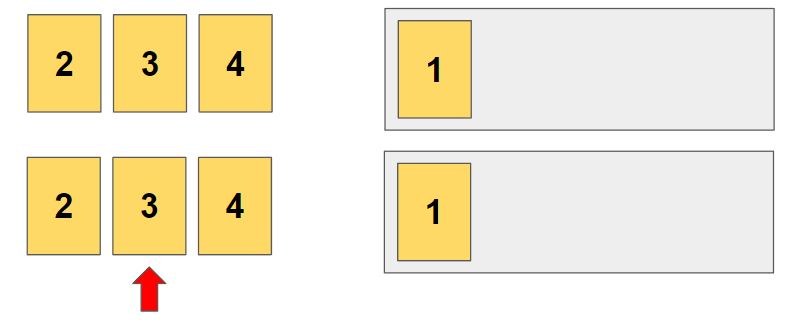
두번째 자리에 3이 들어가는 경우가 시작됩니다.

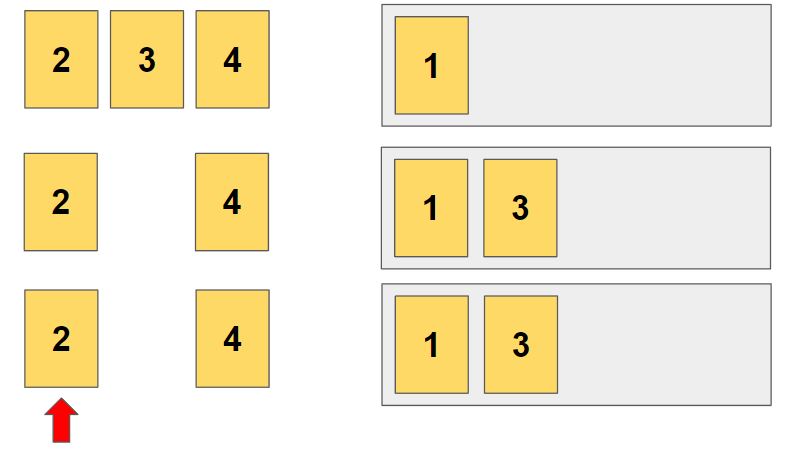
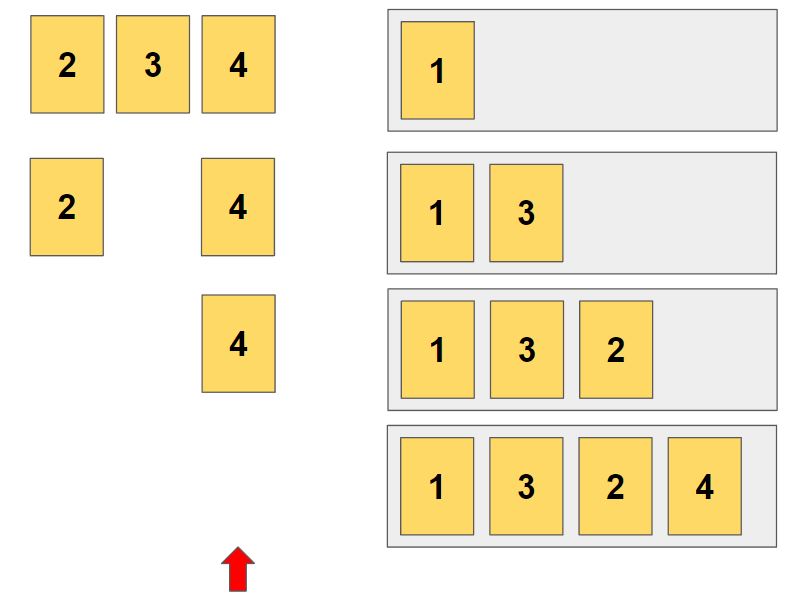
위와 같은 방식으로 진행해서 1-3-2-4 순열을 얻었습니다.

같은 방식으로 진행하면 위와 같은 순서로 24개의 순열을 얻습니다.

처음 시작할때 원소들이 오름차순 정렬된 상태였으므로 결과들도 오름차순으로 정렬된 순서로 나옵니다.

아래는 위 아이디어를 구현한 Java와 Python코드입니다.

size 변수를 number배열의 원소 갯수보다 작게 조절하면 부분순열이 됩니다.

순열을 만드는 방법은 아래와 같이 재귀를 이용한 것과 반복문을 이용한 nextPermutation이란것이 있는데 후자는 다른 포스팅에서 얘기해보도록 하겠습니다.

public class algo_02_permutation {
	static int[] number = { 1, 2, 3, 4, 5, 6 };
	static int size = 6;

	public static void main(String[] args) {
		makePermutation(0, new int[size], new boolean[number.length]);
	}

	public static void makePermutation(int count, int[] picked, boolean[] used) {
		if (count == size) {
			printPermutation(picked);
			return;
		}
		
		for(int i = 0; i < number.length; i++) {
			if(!used[i]) {
				picked[count] = number[i];
				used[i] = true;
				makePermutation(count+1, picked, used);
				used[i] = false;
			}
		}
		
	}

	public static void printPermutation(int[] picked) {
		StringBuilder sb = new StringBuilder();
		sb.append("{ ");
		for (int i = 0; i < size; i++) {
			sb.append(picked[i]).append(" ");
			}
		sb.append("}");
		System.out.println(sb.toString());
	}
}

def makePermutation(count, picked, used):
    global size
    global number

    if(count == size):
        printPermutation(picked)
        return
    
    for i in range(0, len(number)):
        if(not used[i]):
            picked[count] = number[i]
            used[i] = True
            makePermutation(count+1, picked, used)
            used[i] = False
    

def printPermutation(picked):
    global size
    msg = "{ "
    for i in range(0,size):
            msg += str(picked[i])
            msg += " "
    msg += "}"
    print(msg)

number = [1,2,3,4,5,6]
size = 6

makePermutation(0, [0]*size, [False]*len(number))

오랜만에 다시 쓰는 알고리즘 글입니다.

오늘은 부분집합을 만드는 법에 대해 알아보겠습니다.

제가 수학 전공은 아니기 때문에 집합, 부분집합에 관한 기본적인 수학적 지식은 넘기고 설명을 하겠습니다.

부분집합은 어떤 집합에 속한 원소들로만 이루어진 집합입니다.

멱집합은 어떤 집합에서 만들 수 있는 모든 부분집합들을 모은 집합입니다.

보통 부분집합을 응용하는 PS는 이런 멱집합을 구하고 풀이하는 경우가 많습니다.

N개의 원소를 가진 집합의 부분집합의 개수는 2^N개입니다.

부분집합을 만들 때 집합의 어떤 원소를 넣던가 넣지 않던가 두 가지 선택이 가능하고 이런 원소가 N개 있으므로 2^N개의 부분집합이 생기는 것도 당연할 겁니다.

멱집합을 만드는 코드도 이 아이디어를 이용해서 진행합니다.

1~6까지의 숫자를 가진 집합이 있다고 생각해 봅시다.

이 집합의 부분집합으로 하나의 원소를 가진 부분집합 {1}, 여러 원소를 가진 부분집합 {1,2,3}, 공집합 { }, 집합 전체와 같은  {1,2,3,4,5,6}등 여러 종류가 있을 겁니다.

위에서 얻은 아이디어대로 하나의 원소를 넣고 빼는 두 가지 경우를 체크하며 부분집합을 만들어 봅시다.

6개의 원소가 있는 집합이지만 첫 번째 원소 1만 가졌다고 생각해 봅시다.

이 집합의 부분집합은 1이 들어있거나 안 들어있는 두 가지 경우로 나뉩니다.

이 두가지 경우에 대해 우리는 {1}과 { }라는 두 개의 부분집합을 만들 수 있습니다.

두 번째 원소 2를 더해 생각해볼까요?

1과 2 두 개의 원소를 가진 집합의 부분집합은 앞에서 구한 부분집합들에 2가 들어가거나 안 들어가는 두 가지 경우로 생각할 수 있습니다.

즉 우리는 {1,2} {1}, {2}, { }라는 4개의 부분집합을 얻을 수 있습니다.

집합의 원소가 늘어날 때마다 부분집합의 개수는 2배로 늘어나는 것이죠.

3을 포함시켜 {1,2,3}이라는 집합의 부분집합을 구해본다면 앞에서 구한 {1,2} {1}, {2}, { } 4개의 부분집합에 3이 들어가거나 안 들어가는 두 가지 경우로 {1,2,3} {1,3}, {2,3}, {3}, {1,2} {1}, {2}, { } 8개의 부분집합을 만들 수 있을 겁니다.

이렇게 구한 모든 부분집합의 집합을 멱집합이라고 부릅니다.

이 진행과정을 Java와 Python 두 개로 구현해 보았습니다.

부분집합, 조합, 순열 등의 개념을 응용하는 문제는 무척 많기 때문에 익숙해지시면 유용하게 쓰실 수 있습니다.

Java

public class algo_01_subset {
	static int[] number = {1,2,3,4,5,6};
	static int size = 6;
	public static void main(String[] args) {
		makeSubset(0, new boolean[size]);
	}
	
	public static void makeSubset(int idx, boolean[] used) {
		if(idx == size) {
			printSubset(used);
			return;
		}
		
		used[idx] = false;
		makeSubset(idx+1, used);
		used[idx] = true;
		makeSubset(idx+1, used);
	}
	
	public static void printSubset(boolean[] used) {
		StringBuilder sb = new StringBuilder();
		sb.append("{ ");
		for(int i = 0; i < size; i++) {
			if(used[i]) {
				sb.append(number[i]).append(" ");
			}
		}
		sb.append("}");
		
		System.out.println(sb.toString());
	}
}

Python

def makeSubset(idx, used):
    global size
    if(idx == size):
        printSubset(used)
        return
    
    used[idx] = False
    makeSubset(idx+1, used)
    used[idx] = True
    makeSubset(idx+1, used)

def printSubset(used):
    global size
    global number
    msg = "{ "
    for i in range(0,size):
        if(used[i]):
            msg += str(number[i])
            msg += " "
    msg += "}"
    print(msg)

number = [1,2,3,4,5,6]
size = 6

makeSubset(0, [False]*size)

3NF(Third Normal Form) 정규형

3NF 정규형을 만족하려면 릴레이션 내의 이행적 함수 종속을 제거해야 합니다.

이행적 함수 종속은 이전에 설명했듯 (X→Y) 종속관계이고 (Y→Z) 종속관계일때 (X→Z)도 성립하는 경우를 말합니다.

예를 들어 어떤 전자회사의 인적자원을 위와 같은 릴레이션으로 관리할 때, 사원번호를 알면 소속팀을 알 수 있습니다.

그런데 소속부서는 소속 팀을 통해서 알 수 있어 이행적 함수 종속이 발생합니다.

또 이런 이행적 종속으로 인해 이상현상이 발생하게 됩니다.

해결방법은 앞의 다른 정규형들처럼 테이블을 나눠 이행적 종속관계를 없애면 됩니다.

2NF(Second Normal Form) 정규형

2NF 정규형을 만족하려면 릴레이션에서 부분적 함수 종속이 사라지고 완전 함수 종속이 되어야 합니다.

함수 종속성에 대해서는 이전에 정리했으니 릴레이션으로 예시를 들며 설명해 보도록 하겠습니다.

함수종속성에서 예를 들었던 아래와 같은 릴레이션이 있습니다.

이 릴레이션의 기본키는 수업번호입니다.

하지만 과목명은 과목번호에 종속되어 있습니다. 과목번호가 당연히 기본키가 아니기 때문에 이는 부분적 함수 종속성이 있음을 의미합니다.

함수종속성의 설명에서 보았듯 이런 종속성 때문에 튜플의 삽입, 삭제, 갱신에서 이상현상이 발생합니다.

수업이 사라지면 과목의 정보가 사라지기도 하고, 과목명이 바뀌면 해당하는 모든 튜플을 전부 갱신해주어야 합니다.

2NF 정규형을 만족하도록 부분 종속성을 가지는 과목번호와 과목명을 따로 빼어 릴레이션을 나누면

DB를 조작함에서 이상현상이 사라지는것을 알 수 있습니다.

3NF 정규형에 대해서는 다음 글에서 설명해 보도록 하겠습니다.

정규형에는 1부터 5까지의 정규형(Normal Form)과 BCNF(Boyce and Codd Normal Form)가 있습니다.

4NF와 5NF는 간단히 개념만 설명하고 나머지 4개의 정규형을 정규화과정의 예시를 들어 하나씩 설명해 보도록 하겠습니다.

1NF (First Normal Form) 정규형

1NF정규형이 되려면 도메인이 원자값만 가져야 합니다.  

예를 들어 정규화가 되지 않은 아래와 같은 릴레이션이 있습니다.

수강자 어트리뷰트에 학생들의 이름이 여러개 들어있는 걸 볼 수 있습니다.

그런데 김땡땡씨가 조기졸업을 해서 수강자에서 지워져야 한다고 생각해 봅시다.

김땡땡 씨가 있는 튜플을 지우면 다른 수강자들의 정보까지 지워지며 이상현상이 발생합니다.

(과목의 정보도 사라지지만 이건 다음 정규화에서 말하도록 하겠습니다.) 

1NF를 만족시키게 릴레이션을 바꿔 보겠습니다.

수강자 어트리뷰트의 값이 하나만 되도록 튜플을 나누어 주었습니다.

이제 어떤 수강생이 듣는 강의 정보를 지우거나 갱신할 일이 생기더라도 다른 수강자들의 정보엔 영향을 끼치지 않습니다.

2NF에 관해서는 다음 글에서 이어서 설명해 보도록 하겠습니다.

1. 함수종속성

함수적 종속성은 속성들의 집합 두 개 사이의 제약조건입니다.

다시 말해 어떤 릴레이션의 속성 X와 Y가 있을때, 튜플 Y의 값이 X에 의해 결정되거나 종속된다는 것입니다. (X→Y)

또 이 함수 종속성은 세개로 나뉘는데,

완전 함수 종속 : 속성이 기본키에만 종속되고, 기본키가 여러 속성으로 구성된 경우 기본키의 모든 속성에 종속되는 경우. 

부분 함수 종속 : 기본키가 아닌 속성에 종속되거나, 기본키의 일부 속성에 종속된 경우.

이행 함수 종속 : (X→Y) 종속관계이고 (Y→Z) 종속관계일때 (X→Z)도 성립하는 경우.

EX)

대학생의 학생정보를 담은 이런 릴레이션이 있다고 했을때, 이름 학년 학과의 정보는 학번에 종속됩니다. (완전 함수 종속)

이름에도 종속되는게 아니냐 생각할 수도 있지만, 동명이인이 있어 아래와 같은 학생이 존재한다면 이름만 가지고선 학년과 학과 정보를 알 수 없습니다.

따라서 이름은 종속관계를 가지지 않습니다.

대학교 강의 정보를 담은 위와 같은 릴레이션이 있다고 했을때 기본키는 수업번호입니다.

하지만 과목명은 과목번호만 알아도 알아낼 수 있습니다. (부분 함수 종속)

또한 강의실이 수업마다 배정된다면, 강의실도 수업번호에 부분 함수 종속이 됩니다.

2. 이상현상(Anomaly)

이상현상은 릴레이션 안에 같은 데이터가 불필요하게 중복되어 발생하는 현상으로 삽입이상, 삭제이상, 갱신이상의 세가지 종류가 있습니다.

위의 대학교 강의정보 릴레이션을 예로 들어서 설명하겠습니다.

다음 학기부터 새로운 과목인 [데이터사이언스]과목이 신설될 예정입니다. 하지만 아직 수요조사가 끝나지 않아 몇개의 강의가 열릴지 미정된 상태입니다. 그럼 우리는 이 과목을 릴레이션에 등록할때 두 개의 NULL값을 가지게 됩니다. 

또한 강의가 여러개 열린다면 같은 내용의 튜플을 여러개 등록해야겠죠. (삽입이상)

운영체제 강의가 신청자 미달로 폐강되었다고 합시다. 우리는 릴레이션에서 운영체제 수업을 삭제했습니다.

수업이 없어졌을 뿐이지만, 과목번호와 과목명까지도 함께 삭제되었습니다. (삭제이상)

학과 교육과정의 변경으로 과목번호 S100에 해당하는 과목이 데이터베이스에서 [C언어 입문]으로 변경되었습니다.

우리는 과목번호가 S100인 모든 튜플을 찾아서 값을 바꿔주어야 합니다. 예시에선 해당되는 튜플이 단 두개 뿐이지만 수억개의 데이터가 들어있는 실제 사용되는 DB라면 어마어마한 추가 작업이 필요합니다.

3. 정규화

릴레이션에 정보가 중복저장되어 있다면 DB의 가용공간을 낭비할 뿐만 아니라 위에서 보았듯 이상현상이 발생합니다. 이런 문제를 방지하기 위해 정규화 과정을 거칩니다.

예를 들어 위의 강의정보 릴레이션을 정규화 한다면,

이렇게 두개의 릴레이션으로 쪼갤 수 있습니다.

위에서 발생했던 이상현상들을 정규화된 후에 적용시켜 본다면, 새로운 과목을 신설할땐 과목 릴레이션에 S103 - 데이터사이언스 라는 튜플을 추가하면 됩니다. (삽입이상이 발생하지 않음)

또 수업이 폐강되는 경우에도 수업 릴레이션에서 해당하는 수업의 튜플만 지우면 됩니다. 그 수업의 과목정보는 과목 릴레이션에 그대로 남아있습니다. (삭제이상이 발생하지 않음)

과목명이 바뀌는 경우에도 과목 릴레이션에서 해당하는 정보 튜플 하나만 수정하면 그 과목의 수업이 몇개든 상관없이 수정이 완료됩니다.

정규화 단계에 대해선 다음 글로 설명하도록 하겠습니다.

카운팅 소~트 밤 하늘의 퍼얼~ 

오늘은 여섯 번째 정렬 알고리즘이자, 시간 복잡도가 O(N+K)인 특이한 정렬 알고리즘.
계수정렬(Counting sort)에 대해 알아보겠습니다.

1. 데이터의 범위를 전부 표현가능한 자료구조(배열,리스트 whatever)를 준비한다.
2. 데이터를 한 번 순회하면서 각 값의 갯수를 세어준다.
3. 알게 된 갯수만큼 데이터를 저장하거나 출력하면 정렬이 끝!

기존의 정렬들과는 달리 딱 한 번만 데이터를 순회하면 정렬이 완료됩니다.

그림과 함께 정렬의 순서를 확인 해보겠습니다.

1~5 범위의 데이터가 무작위로 준비되어 있습니다.

데이터를 전부 표현 가능한 5 사이즈의 배열을 준비했습니다.

정렬되지 않은 첫 데이터의 값은 3입니다.

값을 셀 배열에서 3의 값을 의미하는 위치의 값을 1 증가시킵니다.

두번째 데이터의 값은 2입니다.

마찬가지로 배열에서 2의 위치의 값을 1 증가시킵니다.

이런 방법으로 데이터를 한 번 순회하면...

위 처럼 정렬되지 않은 데이터가 몇개의 값으로 이루어진지 알 수 있습니다.

이제 값을 센 결과를 통해 정렬된 데이터를 만들어 봅시다.

1의 값을 가진 데이터가 2개이니 2개를 출력(혹은 정렬 후의 배열에 저장)

2의 값을 가진 데이터의 갯수도 2개이니 똑같이 출력

같은 작업을 끝까지 해주면 짠! 하고 정렬된 데이터를 얻게 됩니다.

이해하기도 쉽고 구현도 쉽고 시간복잡도까지 빠른 정렬 알고리즘입니다.

하지만 계수정렬은 특정 상황에서만 유용하게 쓰입니다.

시간복잡도 O(N+K)에서 알 수 있듯, K값인 데이터의 범위에 따라 그 효율성이 크게 달라지기 때문입니다.

예를 들어, 100명이 100점 만점의 시험을 본 점수결과 데이터를 정렬한다고 해봅시다.

K값은 100이고 이 데이터를 정렬하는데엔 대략 200번의 연산이면 충분할겁니다.

반면 100명의 연봉 데이터를 정렬한다고 해봅시다.

100명중에 능력있는 프로그래머가 한 명 있어서 최댓값이 1억이라고 생각해보면 K값은 1억이 되고 이 데이터를 정렬하는데엔 약 1억번의 연산이 필요합니다!

같은 100개의 데이터를 정렬하는데 효율성이 엄청나게 차이가 나죠.

따라서 계수정렬은 특정 상황에서만 유용하게 쓸 수 있는 정렬알고리즘입니다. 

아래는 간단하게 계수정렬을 구현한 JAVA코드 입니다.

디버깅 해보시며 정렬의 흐름을 따라해보시길 바랍니다.

import java.util.Arrays;
import java.util.Random;

public class sort_06_counting {
	static int size = 50;
	static int bound = 10;
	static int count = 0;
	// 데이터의 갯수와 범위 설정

	public static void main(String[] args) {
		int[] data = new int[size];
		Random random = new Random();

		for (int i = 0; i < size; i++) {
			data[i] = random.nextInt(bound);
		}
		// 랜덤 값 넣어주기

		System.out.println(Arrays.toString(data));
		// 랜덤하게 들어간 데이터 확인

		//////////////// 계수정렬 구현코드는 하단으로 /////////////////
		countingSort(data, bound);
		//////////////////////////////////////////////////////

		System.out.println(Arrays.toString(data));
		System.out.println("비교횟수 : " + count);
	}

	private static void countingSort(int[] data, int bound) {
		int[] countingsort = new int[bound + 1];
		int idx = 0;

		for (int i = 0; i < data.length; i++) {
			countingsort[data[i]]++;
			count++;
		}
		
		for (int i = 0; i < bound; i++) {
			count++;
			for(int j = 0; j < countingsort[i]; j++) {
				data[idx++] = i;
			}
		}

	}
}

오랜만에 다섯번째 정렬 알고리즘이자, 시간 복잡도가 O(NlogN)인 정렬 알고리즘.
퀵 정렬에 대해 알아보겠습니다.

1. 데이터 중에서 피봇(pivot)을 뽑습니다.
2. 피봇을 제외한 데이터들을 피봇보다 작은 데이터, 큰 데이터로 분류합니다.
3. 이렇게 두 그룹으로 나뉜 데이터에서 같은 동작을 반복하여 정렬 될 때까지 실행합니다.

퀵 정렬은 설명만 들으면 이해가 되지만 어떻게 이 정렬이 NlogN시간에 정렬이 되는지,

그리고 코드로는 어떻게 작성할지 생각이 막막한 정렬법입니다.

그림과 함께 천천히 알아보도록 하겠습니다.

퀵정렬을 위해 피봇을 정해야합니다.

이번엔 데이터의 정렬되지 않은 그룹의 가장 앞 수를 피봇으로 정해보도록 하겠습니다.

피봇을 정하고 데이터를 순회하면서 피봇보다 작은 수와 큰 수로 나누어줍니다.

계속해서 그룹을 배치해주면...

한 번의 순회가 끝나면, 피봇은 자신의 정렬된 위치에 자리하게 됩니다.

예시 데이터에서 다섯번째로 작은 5는 자신 앞에 위치하는 자기보다 작은 수가 4개임이 당연하므로 자연스럽게 다섯번째 위치에 자리잡게 됩니다.

다음은 피봇으로 나누어진 그룹의 한 쪽에서 다시 한 번 피봇을 정해줍니다.

처음에 약속한대로 가장 앞의 데이터 3을 피봇으로 정합니다.

피봇보다 작은지 큰지에 따라 재배치하면 이런 모양이 됩니다.

5의 경우처럼, 이 그룹에서 세번째에 위치해야하는 3은 자신의 정렬된 위치에 도달한 것을 알 수 있습니다.

5보다 큰 쪽의 그룹도 피봇을 정하고 똑같이 재배치합니다.

두번째 순회가 끝났습니다.

같은 방식으로 1을 피봇으로 잡으면 현 상태 그대로 머물게 되고, 이후 2,4,6,8 하나씩이 남게 된 그룹은 그대로 정렬된 상태가 됩니다.

보시다시피 피봇을 한 번 정할때마다 데이터가 두개로 나뉘고, 전체 데이터를 한 번 순회하면 2^N-1개의 데이터가 정렬되면서 logN번의 순회를 마치면 정렬이 완료되게 됩니다.

한 번 순회할때 데이터를 N개씩 비교하므로 시간복잡도는 NlogN이 됩니다.

(실제로는 매 순회마다 일부 데이터가 완벽히 정렬되므로 비교하는 데이터는 N개보다 적습니다.)

퀵정렬이라는 이름처럼 빠르게 정렬이 완료되는것이죠.

하지만 이런 퀵 정렬에도 예외적인 상황이 있습니다.

이렇게 역순으로 정렬된 데이터를 퀵정렬한다고 생각해 봅시다.

피봇을 가장 앞의 수로 정하고, 순회해서 작은 수의 그룹을 만들었더니... 

마치 버블정렬을 돌렸을 때처럼 피봇을 제외한 모든 수가 되었습니다!

같은 방식으로 피봇을 또 뽑게 되면 또다시 하나의 데이터만 정렬되게 되고, N-1번의 순회가 필요합니다.

그럼 피봇을 다른 방식으로 뽑는다면 어떨까요?

가장 앞의 수 대신 중앙의 수를 골라 피봇으로 선택했습니다.

비교 후엔 우리가 아까 테스트했던 퀵 정렬 처럼 두개의 그룹으로 나뉘며 정렬이 진행되는것을 볼 수 있습니다.

라이브러리에 구현되어 있는 퀵 소트는 이렇듯 피봇이 불리하게 뽑히는 것을 막기 위해 무작위 수로 피봇을 정하는 식으로 예외적인 상황을 회피한다고 합니다.

이렇게 퀵정렬을 통한 정렬이 완료되었습니다!

이건 이해를 돕기 위한 예시일 뿐 실제 코드와 프로그램에선 재귀적으로 파고들어 가며 정렬이 진행되기 때문에 동작 흐름은 다릅니다.

아래는 JAVA로 구현한 간단한 퀻정렬 코드와 테스트입니다!

이것저것 바꿔보고 디버깅하면서 흐름이 이해되시길 바랍니다.

import java.util.Arrays;
import java.util.Random;

public class sort_05_quick {
	static int size = 10;
	static int bound = 1000;
	static int count = 0;
	// 데이터의 갯수와 범위 설정

	public static void main(String[] args) {
		int[] data = new int[size];
		Random random = new Random();

		for (int i = 0; i < size; i++) {
			data[i] = random.nextInt(bound);
		}
		// 랜덤 값 넣어주기

		System.out.println(Arrays.toString(data));
		// 랜덤하게 들어간 데이터 확인

		//////////////// 퀵정렬 구현코드는 하단으로 /////////////////
		quickSort(data, 0, data.length - 1);
		//////////////////////////////////////////////////////

		System.out.println(Arrays.toString(data));
		System.out.println("비교횟수 : " + count);
	}

	private static void quickSort(int[] data, int left, int right) {

		if (left < right) {
			int i = left;
			int j = right;
			int pivot = data[(left + right) / 2];

			while (i < j) {
				while (j >= 0 && data[j] > pivot) {
					j--;
				}
				while (i < j && data[i] < pivot) {
					i++;
				}

				int tmp = data[i];
				data[i] = data[j];
				data[j] = tmp;
				count++;
			}
			// 정렬 과정
			quickSort(data, left, i - 1);
			quickSort(data, i + 1, right);
		}

	}
}